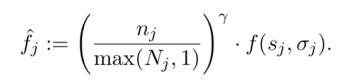
Parameters
Formula break-down
A [n / N'] = ?
B [Ay] = ?
H [B * f(s,o)] = ? (Final result)
Z [(f(s,o) * 100) / C] = ?% (loss)
Explanation
Cardano delegation model includes a mechanism to punish nodes for imperfect performance.
More specifically, if a node (or pool) wins a certain amount of slots N
for an epoch, but misses some of them and creates only n < N blocks.
Then this node will be punished by reducing its total reward (so all the stakeholders
who delegated to the pool are losing profits) and by reducing its rating for future
epoch selections.
This demo-page is for the formula that is used to determine the actual reward of a pool, considering the punishment. This formula is used after the main pool reward formula. This means that at first the "raw" reward is calculated by the main formula, and then this punishment formula is applied to see if the raw reward should be reduced.
Parameters description
"Number of slots owned" (N) - how many slots did the node won at the beginning
of the epoch. These slots are considered to be "owned" by this node, and the node is
supposed to create the same amount of blocks. This number cannot be smaller than
number of created blocks (n).
"Number of created blocks" (n) - how much actual blocks were created
by the node. This number cannot be larger than number of owned slots (N).
"Raw pool rewards" (f(s,o)) - the raw reward, earned by this pool
based on its stake. You can use specific separate
demo page to see how this works.
"penalty severity" (y) - a system constant. This parameter determines,
how severely the node will be punished depending on how many slots are missed.
You can see different values of this parameter being plotted on the chart.
Sources
This formula is taken from the official reward scheme paper: Calculator Documentation
Charts
Explanation
These two charts show how resulting pool reward is affected by changing
h and y values. You can try changing the y
value and see how charts respond.
Different y as n grows (left or top chart)
On this chart you can see different values of y being plotted
at different number of blocks (n) being created. Each line represents
a different system, where constant y is selected at different value.
You can change the number of slots (N) value in the input form and see
how chart changes.
Chart clearly shows that at n=0 any value of y gives
the resulting reward of 0 (except the very special case of y=0,
which means that no punishment will be applied at all). This means that no matter
what is the punishment severity - it is impossible to get a reward for making no
blocks at all.
Next you can clearly see a straight middle line that goes diagonally between bottom-left
and top-right corners. This line represents value of y=1 when punishment
is perfectly proportional to the performance - if a node has created 50% of it's blocks,
then it will receive 50% of raw rewards, etc.
All lines above the middle-line represent values of y < 1.
You can see how with these values node would receive lower punishment at higher
number of created blocks (few missed blocks), but then as number of created blocks
goes down - punishment gets more severe, resulting in the same zero value.
On the other side, all lines under the middle-line represent values of
y > 1 and bend in opposite direction. This means that the larger
value of y gets - the more severely punished first missed slots become.
You can see how at y=10 first 5 missed blocks (n=95)
already gets the node only ~60% of the raw reward.
Different N as n grows (right or bottom chart)
On this chart each line represents a node\pool with different amount of slots
they have won for the passed epoch, and x-axis represents how many blocks they
have actually created. So leftmost line represents a pool that have won 20 slots
(or 20% of slots, if you have N>100). You cann see 5 points on this line,
representing its reward if has produced: 0, N/4, N/2,
3N/4, or N blocks. All other lines represent similar steps
for nodes with larger amount of owned slots.
If you change the y value in the input form, you will see the chart respond.
Doing so you can clearly notice the "middle-line" of rewards, consisting of points
representing 50% of blocks in the middle of each line (this middle-line falls exactly
at 50% reward at y=1). So you can move y value around
and see, how nodes of different size would be relatively compensated if they miss
a quoter, or a half of its slots.
Conclusions
Selecting right y value is a complex task, because it determines the
"forgiveness" of the system. With smaller values of y nodes can
easier miss few blocks and not lose that much profits, but again as number
of created blocks goes down - mild y appears to be less and less fair,
because even by missing 50% of slots nodes still receive >50% of rewards.
On the other hand, larger values of y impose more severe punishment
for nodes as they miss more blocks, but at the same time it may cause the punishment
to be "too severe" for small nodes that miss few blocks.
Right value is for the IOHK to select, depending on what kind of behaviour they want to model for the system.